This project is to develop a model-free reinforcement learning method for stochastic planning under temporal logic constraints. Using temporal logic formulas instead of reward function, we can rigorously express the desired properties to be achieved in the learned policies for stochastic systems. It will also provide provable performance guarantees in the controller learned from RL algorithms. With Temporal Logic, we can specify tasks such as, “visiting a sequence of waypoints A, B,C,D while avoiding obstacles”, “if the region A is visited, then region B must be visited before region C”, “if the probability of reaching A is less than 0.2, then only B,C,D need to be visited with a probability greater than 0.7.”, and logical compositions of these properties.
- Probabilistic Planning with constraints in PCTL: In recent work [1], we propose an approach to translate high-level system specifications expressed by a subclass of Probabilistic Computational Tree Logic (PCTL) into chance constraints. We devise a variant of Approximate Dynamic Programming method—approximate value iteration— to solve for the optimal policy while the satisfaction of the PCTL formula is guaranteed.
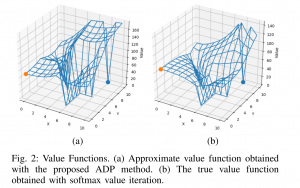
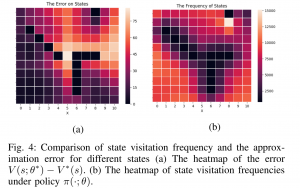
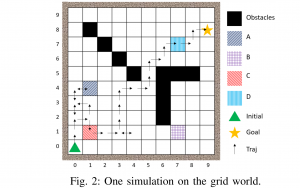
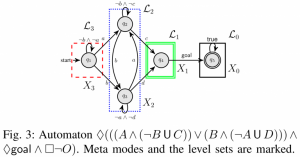
- Exploiting the structure of automata to enable data- and sample- efficient RL for LTL formulas: In [2], we study model-free reinforcement learning to maximize the probability of satisfying high-level system specifications expressed in a subclass of temporal logic formulas—syntactically co- safe linear temporal logic. In order to address the issue of sparse reward given by satisfaction of temporal logic formula, we propose a topological approximate dynamic programming which includes two steps: First, we decompose the planning problem into a sequence of sub-problems based on the topological property of the task automaton which is translated from a temporal logic formula. Second, we extend a model-free approximate dynamic programming method to solve value functions, one for each state in the task automaton, in an order reverse to the causal dependency. Particularly, we show that the run-time of the proposed algorithm does not grow exponentially with the size of specifications. The correctness and efficiency of the algorithm are demonstrated using a robotic motion planning example.
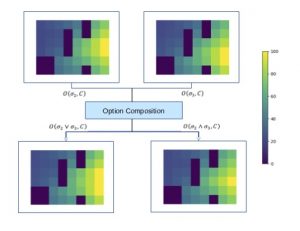
- Hierarchical Probabilistic Planning as Logical Composition: In [3], we combine hierarchical planning with logical compositional reasoning for improving the scalability of RL with temporal logic taskspecifications. This is because, in practice, scalability poses the main barrier for many systems since the size of policy grows exponentially in the size of the specification formula. To tackle this issue, we proposed a compositional planning approach that decomposes the original temporal logic-constrained planning problem to several problems with smaller and simpler specifications. By establishing the relations between compositional reasoning in quantitative temporal logic and composability of a class of near-optimal policies called entropy-regulated optimal policies, we develop an algorithm that is able to generate modular sub-policies under the set of simple specifications and further reuse and compose them to solve for a good initial policy under the original specification. Moreover, based on the option framework in hierarchical MDP planning, the optimal policy can be obtained efficiently via planning with both primitive actions, sub-policies, and the ‘compositions’ (or precisely, arbitration) of sub-policies.
Example of composition: Consider the robot wants to visit regions labeled 1,2,3 in a given order. the options include the optimal policies for reaching regions 1, 2, 3. The composed policy is based on generalized logical composition to construct the semi-optimal policy for reaching 1 OR 2 by composing the two options of reaching 1 , reaching 2, using a composition rule specified in paper [3], instead of recomputing a new policy for the task.
Project Opportunities: Based on the existing work, we are interested in exploring integrating preference logic and temporal logic for preference-based decision-making in stochastic environments. If you are interested in this direction, please reach out to Dr. Jie Fu for more information.
Related Publications:
[1] Lening Li, Jie Fu, “Approximate Dynamic Programming with Probabilistic Temporal Logic Constraints”, arXiv:1810.02199, Annual American Control Conference, 2019.
[2] Lening Li, Jie Fu, “Topological Approximate Dynamic Programming under Temporal Logic Constraints”, arXiv: 1907.10510, IEEE Conference on Decision and Control, 2019.
[3] Xuan Liu, Jie Fu, “Compositional Planning in Markov Decision Process: Temporal abstraction meets generalized logic composition”, arXiv:1810.02497 math.OC, American Control Conference, 2019.
[4]Lening Li, Jie Fu, “Sampling-based approximate optimal temporal logic planning”, IEEE International Conference on Robotics and Automation (ICRA), 2017.
[5] Ivan Papusha, Jie Fu, Ufuk Topcu, and Richard M. Murray, “Automata Theory Meets Approximate Dynamic Programming: Optimal Control with Temporal Logic Constraints”, IEEE Conference on Decision and Control, 2016. pdf
[6] Jie Fu and Ufuk Topcu, “Computational methods for stochastic control with metric interval temporal logic specifications,” IEEE Conference on Decision and Control, 2015. pdf
[7] Jie Fu, Shuo Han, and Ufuk Topcu, “Optimal control in Markov decision processes via distributed optimization,” IEEE Conference on Decision and Control, 2015. pdf
[8] Jie Fu and Ufuk Topcu, “Pareto efficiency in synthesizing shared autonomy policies with temporal logic constraints.” IEEE International Conference on Robotics and Automation, 2015. pdf
[9] Jie Fu and Ufuk Topcu, “Probably approximately correct MDP learning and control with temporal logic constraints”, Robotics: Science and Systems, 2014. pdf